1. ホーム
2. ＞統計解析・品質管理
3. ＞製品案内
4. ＞手法一覧

最尤推定（MLE）とは（信頼性解析）

故障時間データに対し，分布のパラメータを求める推定法として最尤推定法があります．

最尤推定法（maximum likelihood estimate method）とは，尤度を「手持ちの観測データのもとで，あるパラメータ値が得られる確率」とみなして，尤度を最大化するようなパラメータ値を探索する推定方法です．即ち，確率論的モデルのパラメータを変えていって，観測データにもっともよく「あてはまる」ところを探索していく方法です．

最尤推定法は，尤度関数が線形な方程式の場合に，計算式を用いて解析的に値を求めることができるので，多くの場面でよく用いられる推定法です．また，最尤推定量はサンプル数が多い時に，精度の良い推定量となります．

よくあるご質問（信頼性解析）FAQをもっと見る

• 資料用に正規分布曲線を描きたいです．StatWorksに正規分布曲線を描く機能はありますか？

最尤推定（MLE）の使用方法

1．データの用意

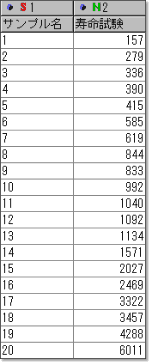
図1．寿命試験のデータ

20個の部品が故障した時間を並べた寿命試験のデータがあります．

1列目はサンプル名，2列目は寿命試験で各サンプルが壊れた故障時間です．

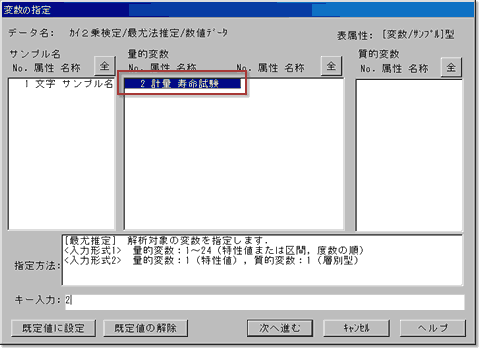
2．変数の指定

メニューバーから[手法]-[信頼性解析] -[分布型の検定・推定]-[最尤推定]を起動します．変数の指定画面で量的変数の「寿命試験」を指定します．

図2．変数の指定

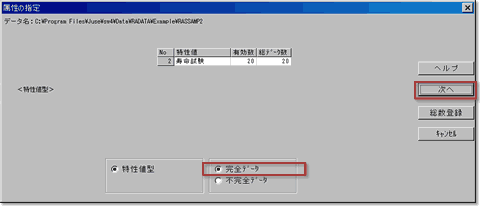
3．属性の指定

今回は完全データ※を扱うので，属性の指定で「完全データ」を指定し，「次へ」ボタンを押します． ※ 完全データとは，n個のサンプルの寿命（故障時間）データから寿命分布を推定しようという場合に，n個すべてのデータが得られたものです．これに対して何らかの原因で一部のデータしか得られないものは，不完全データといいます．

図3．属性の指定

4．分布の選択

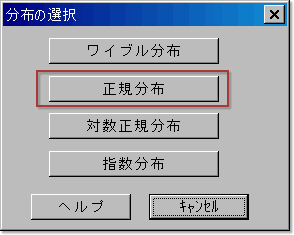
図4．分布の選択

データが従っていると思われる分布を選択します．

ここでは，データは正規分布に従っていると仮定して，そのパラメータを求めることにします．「分布の選択」ダイアログで「正規分布」をクリックします．

5．パラメータの推定

正規分布のパラメータ（平均，標準偏差）とMTTF（Mean Time To Failure：故障までの平均時間）が求められました．

図5．パラメータの推定

本システムの機能・特徴

分布の切り替え

画面左上の「分布」のリストで，分布を切り替えることができます．本システムで扱える分布はワイブル分布，正規分布，対数正規分布，指数分布です．ワイブル分布は，収束計算の初期値及びずらしの値の入力が可能となっています．

---

※ 「画面はJUSE-StatWorks/V4.0のものです」

無料体験版をダウンロード

こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．

統計的手法を身につけ，実務に生かす

イベント・セミナーのご案内

JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．

【セミナー】信頼性データ解析入門

信頼性データ解析に必要な解析技術と基礎知識，統計ソフトの使い方などを短期間に習得できます．

【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）

統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．

eラーニングシステム『StatCampus』のご案内

原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）

自習や集合研修に…関連書籍

実務に役立つシリーズ 第3巻 『信頼性データ解析入門』
	信頼性データ解析を実務で活用するための手引き
	棟近雅彦 監修 / 関哲朗 著
	定価 3,080円（税込）
	サンプルデータ公開中　ダウンロードへ