信頼度・故障率曲線とは（信頼性解析）
信頼度曲線とは縦軸に信頼度，横軸に時間をとったグラフ上に，プロット点の結線処理を施すなどして，信頼度の推移の傾向を見たものです．
信頼度：通常R(t)と表記します．ある時間tまでに故障しないものが全体に対してどのくらい残っているかを示すもので0.0～1.0の値をとります．不信頼度（累積故障率）F(t)との関係は，R(t)＝1-F(t)となっています．
故障率曲線とは縦軸に故障率，横軸に時間をとったグラフ上に，プロット点の結線処理を施すなどして，故障率の推移の傾向を見たものです．
故障率：通常λ(t)と表記します．ここでの故障率は区間故障率であり，λ(t)＝区間⊿tの故障数／（区間⊿tの長さ×区間開始時点の残存数）と計算され，0.0～1.0の値をとります．
使用例
1．データの用意
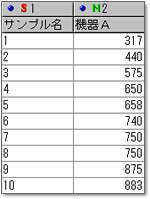
図1．10個の故障データ
10個の故障データがあります．
1列目はサンプル名（サンプル名），2列目は機器Aにおける故障時間（量的変数）です．
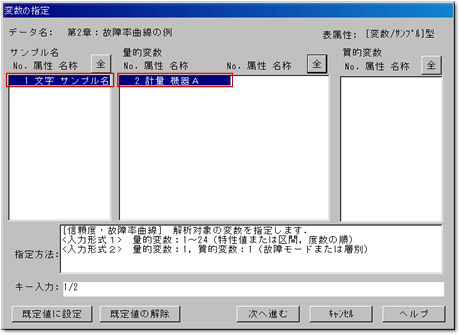
2．変数の指定
メニューバーから[手法] - [信頼性解析] - [グラフによる観察] - [信頼度・故障率曲線]を起動します．変数の指定画面でサンプル名の「サンプル名」，量的変数の「機器A」を指定します．
図2．変数の指定
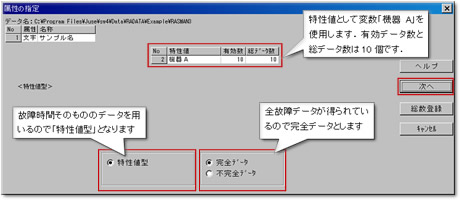
3．属性の指定
「属性の指定」ダイアログが表示されますので，信頼度・故障率曲線に表示させる内容の確認をおこないます．
量的変数を2つ以上使用する場合は，データが特性値型（故障時間そのもののデータ）か区間・度数型（故障時間データをある時間間隔で集計したもの）かを選択しますが，ここでは量的変数が1つなので特性値型となります．また，ワークシート上の10個のデータが全故障データなので，「完全データ（※）」を指定します．
正しく設定されていることを確認し，「次へ」ボタンを押します．
※ 完全データとは，n個のサンプルの寿命（故障時間）データから寿命分布を推定しようという場合に，n個すべてのデータが得られたものであり，これに対して何らかの原因で一部のデータしか得られないものは，不完全データといいます．
図3．属性の指定
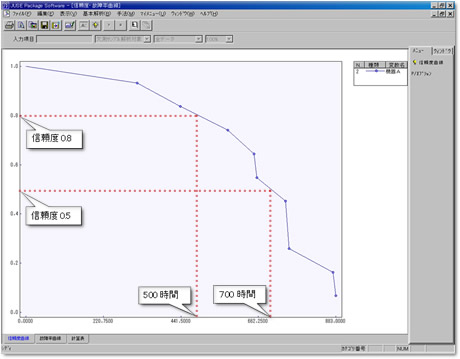
4．信頼度曲線の表示（横軸：時間，縦軸：信頼度）
横軸に時間，縦軸に信頼度をとった信頼度曲線が表示されます．このグラフから，信頼度が0.8，すなわち全体の80%が故障した時間が500時間程度であり，信頼度が0.5，すなわち全体の半分が故障した時間が700時間程度であることが読み取れます．
図4．信頼度曲線の表示（横軸：時間，縦軸：信頼度）
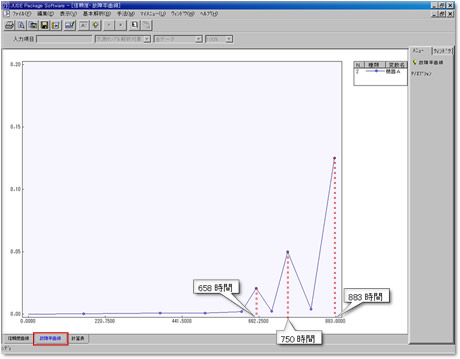
5．故障率曲線の表示（横軸：時間，縦軸：故障率）
「故障率曲線」のタブを選択すると，横軸に時間，縦軸に故障率をとった故障率曲線を表示します． このグラフから，時間658，750，883で故障率が高くなっていることが読み取れます．
図5．故障率曲線の表示（横軸：時間，縦軸：故障率）
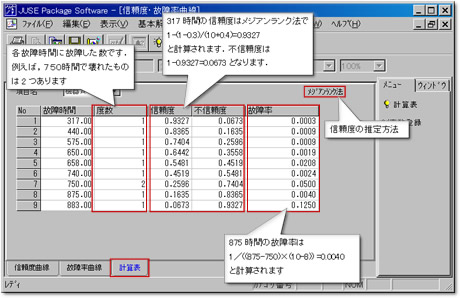
6．メディアンランク法による推定
「計算表」のタブを選択すると信頼度，不信頼度，故障率が数値で確認できます．
画面右上に「メディアンランク法」とありますが，これは信頼度の推定方法です．メディアンランク法の信頼度の推定式は1-(r-0.3)/(n+0.4)となっています．故障率は前述の通り，λ(t)＝区間⊿tの故障数／（区間⊿tの長さ×区間開始時点の残存数）と計算されます．
他の信頼度の推定法として平均ランク法や累積ハザード法が使用できますが，変更するには「信頼度曲線」ウィンドウか「故障率曲線」ウィンドウ上でメニューボタン「オプション」を押し，推定法の設定をします．
図6．メディアンランク法による推定
本システムの機能・特徴
- オプション指定
- 「信頼度曲線」ウィンドウもしくは「故障率曲線」ウィンドウでメニューボタン「オプション」を押すと，目盛や結線・近似曲線の指定ができます．X軸目盛は対数変換したものにすることもできます．結線・近似曲線は「プロット点のみ」，「折線」，「直線」，「スプライン（点を結ぶ滑らかな曲線）」から選択できます．
※ 「画面はJUSE-StatWorks/V4.0のものです」
無料体験版をダウンロード
こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．
統計的手法を身につけ，実務に生かす
イベント・セミナーのご案内
JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．
- 【セミナー】信頼性データ解析入門
- 信頼性データ解析に必要な解析技術と基礎知識，統計ソフトの使い方などを短期間に習得できます．
- 【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）
- 統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．
- eラーニングシステム『StatCampus』のご案内
- 原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）
| 実務に役立つシリーズ 第3巻 『信頼性データ解析入門』 | |
|---|---|
 |
信頼性データ解析を実務で活用するための手引き |
| 棟近雅彦 監修 / 関哲朗 著 | |
| 定価 3,080円（税込） | |
| サンプルデータ公開中 ダウンロードへ | |
イベント案内や製品などの最新情報をお届けします