1. ホーム
2. ＞統計解析・品質管理
3. ＞製品案内
4. ＞手法一覧

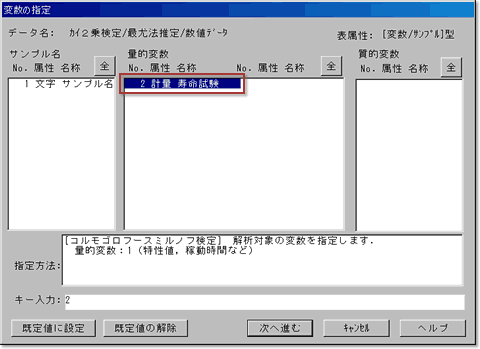
1標本K-S検定とは（信頼性解析）

1標本K-S検定（コルモゴロフ-スミルノフ検定：Kolmogorov-Smirnov test）はデータの分布への適合性の検定方法です．サンプルの累積分布関数が，仮定した分布の上限・下限内に入っているかどうかを見て検定を行います．

1標本K-S検定は少数サンプルの場合も有効です．同じく分布への適合性の検定方法であるカイ二乗検定はサンプル数が十分に大きい必要があるため，一般的に，サンプル数が30以下の時は，1標本K-S検定の方を用います．

1標本K-S検定の使用方法

1．データの用意

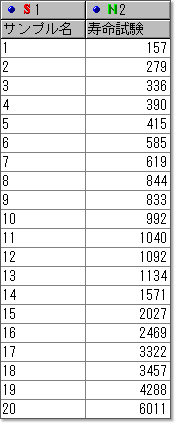
図1．寿命試験のデータ

20個の部品が故障した時間を並べた寿命試験のデータがあります．

1列目はサンプル名，2列目は寿命試験で各サンプルが壊れた故障時間です．

2．変数の指定

メニューバーから[手法]-[信頼性解析] -[分布型の検定・推定]-[最尤推定]を起動します．変数の指定画面で量的変数の「寿命試験」を指定します．

図2．変数の指定

3．属性の指定

今回は完全データ*1を扱うので，属性の指定で「完全データ」を指定し，「次へ」ボタンを押します．

図3．属性の指定

*1

完全データとは，n個のサンプルの寿命（故障時間）データから寿命分布を推定しようという場合に，n個すべてのデータが得られたものであり，これに対して何らかの原因で一部のデータしか得られないものは，不完全データといいます．

4．推定方法の選択

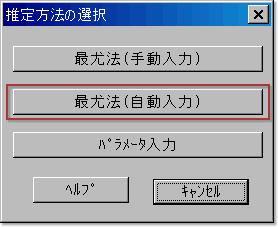
図4．推定方法の選択

分布のパラメータについて設定します．

予めパラメータが分かっている場合には，「パラメータ入力」を選択し，自分でパラメータを入力します．初期値を与えた上で，最尤法でパラメータを推定したい場合には「最尤法（手動入力）」，初期値は特に与えずに最尤法で推定したい場合には「最尤法（自動入力）」を選択します．

ここでは，最尤法（自動入力）で推定することにします．

5．分布型の選択

図5．分布型の選択

データが従っていると思われる分布を選択します．ここでは，データは正規分布に従っていると仮定し，「分布の選択」ダイアログで「正規分布」をクリックします．

6．計算表の確認

「計算表」のタブでは計算表が確認できます．データが仮定した分布に従う時の下限F0(x)-Dと上限F0(x)+Dが計算されています．また，各 サンプルの累積分布関数をi/nで求めています．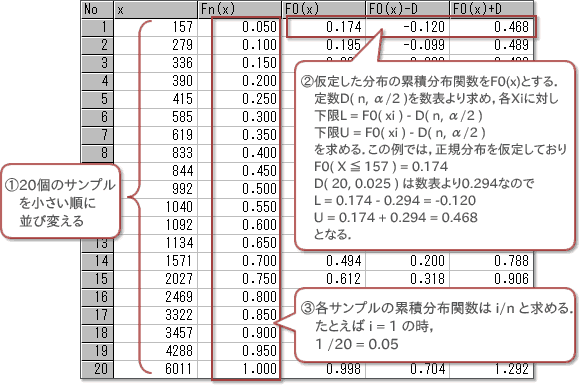

図6．計算表の確認

7．検定結果の確認

「確率紙」のタブに1標本K-S検定の検定結果が表示されます．

サンプルの累積分布関数（太線）が仮定した分布の下限（下側の青い線）と上限（上側の青い線）の間に入っていれば「仮定した分布に適さないとはいえない」となり，1つでも上限と下限の間に入っていなければ「仮定した分布に適しているとはいえない」ということになります．

今回は，サンプルの累積分布関数は下限と上限の間に入っており，帰無仮説「H0：正規分布に従っている」は有意水準0.05で棄却されませんでした．つまり，今回のデータは「正規分布に従っていないとはいえない（正規分布に従っていそうだ）」という結果になりました．

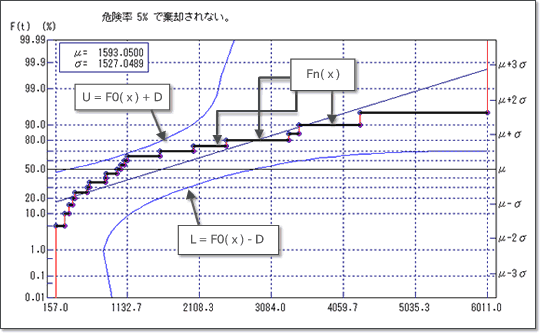
図7．検定結果の確認

---

※ 「画面はJUSE-StatWorks/V4.0のものです」

無料体験版をダウンロード

こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．

統計的手法を身につけ，実務に生かす

イベント・セミナーのご案内

JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．

【セミナー】信頼性データ解析入門

信頼性データ解析に必要な解析技術と基礎知識，統計ソフトの使い方などを短期間に習得できます．

【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）

統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．

eラーニングシステム『StatCampus』のご案内

原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）