1. ホーム
2. ＞統計解析・品質管理
3. ＞製品案内
4. ＞手法一覧

カイ二乗検定とは（信頼性解析）

カイ二乗検定（chi-square test）はデータの分布への適合性の検定方法です．サンプルをいくつかのクラスに分類して行います．

近似的な方法であるため，サンプル数が十分に大きくなくてはなりません．一般的に，サンプル数は30以上必要と言われます．

カイ二乗検定の使用方法

1．データの用意

図1．電気機器のデータ

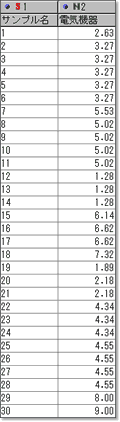
30個の電気機器が故障した時間を並べたデータがあります．

1列目はサンプル名，2列目は電気機器の故障時間です．

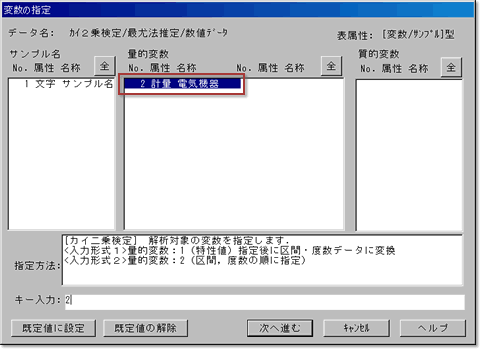
2．変数の指定

メニューバーから[手法]-[信頼性解析] -[分布型の検定・推定]-[K-S検定]を起動します．変数の指定画面で量的変数の「寿命試験」を指定します．

図2．変数の指定

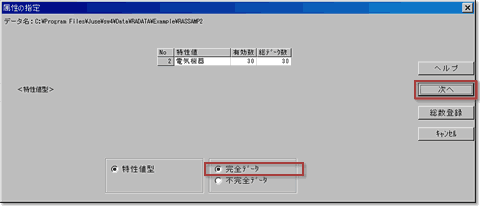
3．属性の指定

今回は完全データ*1を扱うので，属性の指定で「完全データ」を指定し，「次へ」ボタンを押します．

図3．属性の指定

*1

完全データとは，n個のサンプルの寿命（故障時間）データから寿命分布を推定しようという場合に，n個すべてのデータが得られたものであり，これに対して何らかの原因で一部のデータしか得られないものは，不完全データといいます．

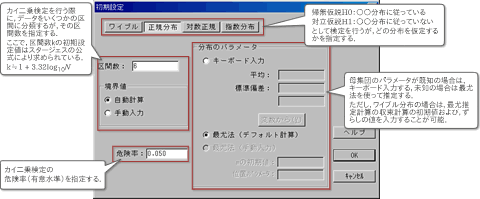
4．初期設定

「初期設定」ダイアログで，検定に関する初期設定を行います．

仮定する分布と区間数，検定の危険率（有意水準），分布のパラメータの与え方を指定します．例えばここでは，分布は正規分布，区間数は6，危険率（有意水準）は0.05，分布のパラメータは最尤法（デフォルト計算）で推定する，と設定して，「OK」ボタンをクリックします．

図4．初期設定

5．計算表の確認

カイ二乗検定の計算表を確認します．

ここで，カイ二乗検定では1つの区間に含まれるデータの数は5以上でなければならないことに注意します．5以下になるときには隣接の区間はマージ（統合）して5以上になるようにします．

本例では5.14≦X 6.43，6.43≦X 7.71，7.71≦Xの3区間に入る度数がそれぞれ，2，3，2となりいずれも5以下であるので，区間をマージして，区間に含まれる度数を5以上にします．

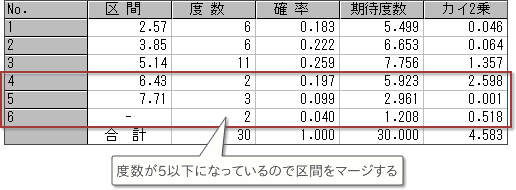
図5．計算表の確認

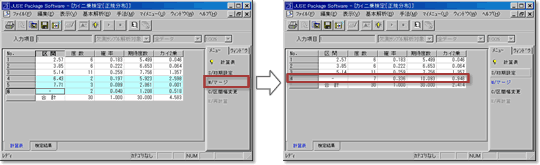
6．区間のマージ

統合する区間の行をクリックすると選択され，行が着色されます．

行が着色された状態でメニューボタン「マージ」を押します． 区間がマージされ，1つの区間に含まれるデータの数が5以上になりました．

図6．区間のマージ

7．計算表の確認（2）

マージ後の計算表を確認します．各区間の度数と期待度数から，カイ二乗統計量が計算されています．

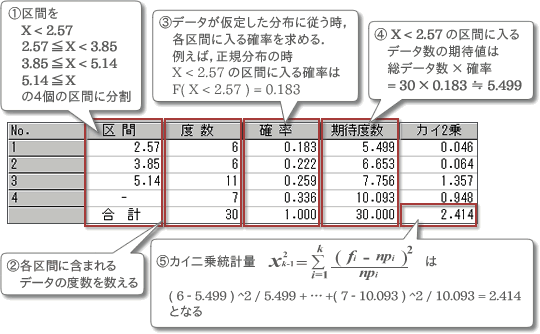
図7．計算表の確認（2）

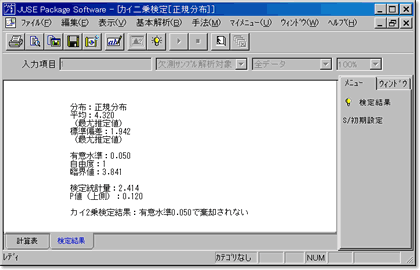
8．検定結果の確認

「検定結果」のタブにカイ二乗検定の検定結果が表示されます．

カイ二乗検定の結果，帰無仮説「H0：正規分布に従っている」は有意水準0.05で棄却されませんでした．つまり，今回のデータは「正規分布に従っていないとはいえない（正規分布に従っていそうだ）」という結果になりました．

図8．検定結果の確認

---

※ 「画面はJUSE-StatWorks/V4.0のものです」

無料体験版をダウンロード

こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．

統計的手法を身につけ，実務に生かす

イベント・セミナーのご案内

JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．

【セミナー】信頼性データ解析入門

信頼性データ解析に必要な解析技術と基礎知識，統計ソフトの使い方などを短期間に習得できます．

【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）

統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．

eラーニングシステム『StatCampus』のご案内

原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）

自習や集合研修に…関連書籍

実務に役立つシリーズ 第3巻 『信頼性データ解析入門』
	信頼性データ解析を実務で活用するための手引き
	棟近雅彦 監修 / 関哲朗 著
	定価 3,080円（税込）
	サンプルデータ公開中　ダウンロードへ