1. ホーム
2. ＞統計解析・品質管理
3. ＞製品案内
4. ＞手法一覧

二元配置分散分析とは（実験計画法）

二元配置分散分析は，ある特性値に対して，2つの因子の影響を調べる場合に用いる手法です．ある特性値に影響を及ぼすと考えられる原因のうち，2つの因子A（l水準），因子B（m水準）を選び，各水準の組合せ（l，m通り）における繰り返し数をr回とした場合，全部でl×m×r回の実験をおこないます．この時，実験の順序は完全にランダムに行う必要があります．このような実験を二元配置実験と呼びます．

ここで，r=1の場合には，因子A，Bに関し，l×m通りの組合せがありますが，これらをランダムに1回ずつ行う場合を繰り返しのない二元配置と呼び，r≧2の場合を繰り返しのある二元配置と呼びます．

二元配置では，因子がAとBの2つになるため，AとBの主効果のほかに，A，Bの組合せによる交互作用と呼ばれる効果を考慮する必要があります．また，繰り返しのある二元配置では，交互作用を誤差と分離して求めることができるため，交互作用の存在が予測される場合には，繰り返しのある二元配置実験を行うとよいでしょう．

---

実験計画手法（DOE）の考え方，またソフトを使う上での利点についての資料をご覧いただけます．

(株)日本科学技術研修所のシンポジウムでの製品紹介

設計開発に役立つ実験計画法～要因配置実験から応答曲面まで～

本システムの機能・特徴

二元配置分散分析の機能

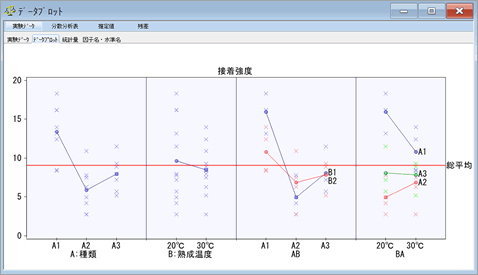
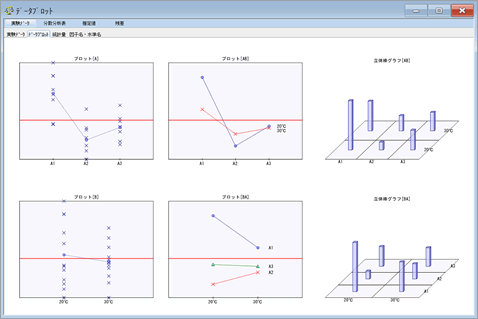
実験データ	データプロットのウィンドウが表示されます．各因子の主効果や交互作用などを視覚的に確認することができます．「グラフ種類指定」のオプションから，「データプロット」の表示方法を切り替えることができます．
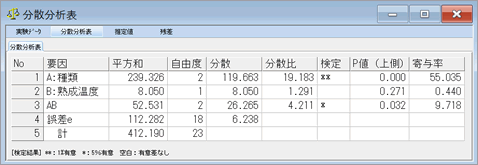
分散分析表	要因Aおよび誤差項に対し，平方和，自由度，不偏分散，分散比，検定結果，寄与率などを表の形にして表示します．各要因あるいは交互作用について，誤差に対して各水準の母平均に有意な差があるかどうかを検定します．説明のため，仮に各因子をA，B，交互作用をA*BとするとSA，SB，SA*B，Seをそれぞれの自由度φA，φB，φA*B，φeで割ってVA，VB，VA*B，Veを求め，不偏分散の比を各A，B，A×Bにて求めます． Aの場合を例にとり説明すると，データから計算されたF0=VA/Ve，を自由度φA，φeのF分布の上側α%の値F（φA，φe，α）より大きくなるかどうかを判定します．本システムでは，このα（危険率）を5%または1%として検定します．また，寄与率(各要因効果の全変動に占める割合)も表示することができます．
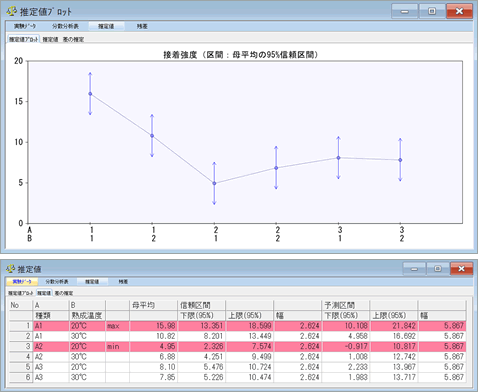
推定値	分散分析の結果，有意と判断された場合，具体的にどの水準の平均が高く，どの水準が低いかは不明です．そこで，各水準の母平均の推定を行います．推定値プロットでは，各水準ごとに母平均と信頼区間を推定し，視覚的に確認を行うことができます．推定式に交互作用を取り入れる／取り入れないも選択できます(表示因子が2因子のとき)．
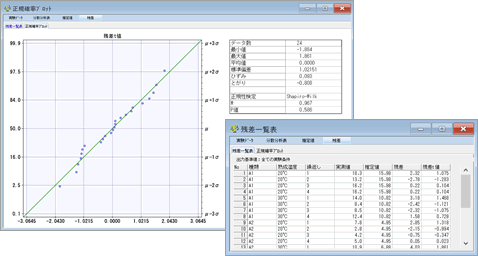
残差	データの中に異常値や外れ値が含まれているかどうかのチェックを行います．表示させたい残差t値の基準値を，自由に指定できます．正規確率プロットで確認することもできます．

出力画像（画像クリックで拡大サイズへ）

• 
  「データプロット・立体棒グラフ」
• 
  「要因ごとのデータプロット」
• 
  「分散分析表」
• 
  「推定値プロット」と「推定値」
• 
  「残差一覧表」と「正規確率プロット」

無料体験版をダウンロード

こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．

統計的手法を身につけ，実務に生かす

イベント・セミナーのご案内

JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．

【セミナー】データ解析入門 実務で使える実験計画法

実験計画法の手法の目的や考え方，活用方法を理解・習得するコースです．

【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）

統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．

eラーニングシステム『StatCampus』のご案内

原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）

自習や集合研修に…関連書籍

JUSE-StatWorksによる新品質管理入門シリーズ 第3巻 『実験計画法入門』
	「実験計画法」の手法の考え方と，数理展開の解説
	棟近雅彦 編著 / 奥原正夫 著
	定価 3,300円（税込）
	書籍用体験版とサンプルデータ公開中　ダウンロードへ