1. ホーム
2. ＞統計解析・品質管理
3. ＞製品案内
4. ＞手法一覧

SEM(構造方程式モデリング)とは（因果分析）

SEMとは「構造方程式モデリング」または「共分散構造分析」と呼ばれ，重回帰分析や因子分析，パス解析などの機能を併せ持つ統合手法として，従来の多変量解析を超えた一歩進んだ解析手法です．

現在マーケティングや社会調査，心理学などの分野でよく利用されておりますが，技術開発や製造工程のデータ分析，新商品開発における「意識調査分析」「品質改善活動」など，ものづくりや理工学系の研究や教育においても有効な手法です．

構造方程式モデリングでは，パス図を用いて変数間の因果関係を表します．矢線で表したパス図により，難しい統計モデルの構造をビジュアルでわかりやすく表現することができます．

---

「JUSE-StatWorks/V4.0 SEM因果分析編 製品発表説明会」で発表された公開資料をご覧いただけます．

椿 広計氏（元・筑波大学 教授/現・統計数理研究所 教授）による基調講演

「共分散構造分析は，自然科学からモノつくりへ」

野中 英和氏（TDK株式会社）による事例報告

「製造データの因果分析」 -SEMとグラフィカルモデルを使った要因解析-

SEM(構造方程式モデリング)の使用方法

構造方程式モデリングは以下の手順で解析を行います．

日本品質管理学会 テクノメトリックス研究会（1999）『グラフィカルモデリングの実際』
日科技連出版社，P189-196事例「IC製造工程の分析」より引用

1.仮説に基づき変数（観測変数，因子）間の関係をモデル化します

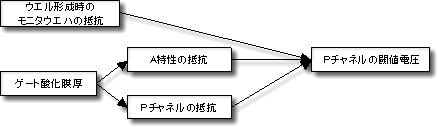
2.構築したモデルをデータに当てはめます

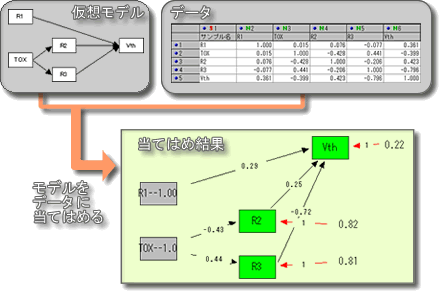
3.考察と修正

モデルがデータに適合していれば，そのモデルから考察をおこないます．適合していなければ仮説モデルを修正します．

よくあるご質問（因果分析）FAQをもっと見る

• SEMで解が収束しない場合，どうすればよいでしょうか？

本システムの機能・特徴

本システムの有用性をまとめると，以下の3点になります．

I. 仮説モデルが収集データに適合しているかどうかを検証することができます

構造方程式モデリングは，仮説に基づき変数間の関係をモデル化し，構築したモデルをデータに当てはめます．ここで，モデルがデータに適合していればそのモデルから考察をおこない，適合していなければモデルを修正します．

本システムでは仮説モデルをデータに基づき検証できることが特徴の1つです．

II. 様々な仮説モデルを考え，比較することができます

構造方程式モデリングでは，従来の多変量解析手法から更に一歩進んだ解析をおこなうことができます．構造方程式モデリングは仮説モデルを検証することが主な目的となりますが，構造方程式モデリングという枠組みの下で様々な仮説モデルを分析・検証することができます．

例えば，パス解析は重回帰分析の拡張と捉えることができ，目的変数と説明変数の間の関係だけではなく，説明変数間の関係も考えることができます．また，重回帰分析，因子分析など通常使用される多変量解析手法ではおこなうことができなかった潜在変数を含むデータ構造の関係を分析することができます．

III. 複数の母集団（グループ）を同時に分析し，母集団の比較を行うことができます

本システムでは多母集団モデルの分析を行うことができます．

複数の母集団（例えば，男性や女性，薬剤AとBなどの層別情報）から得られたデータを分析する場合，これらの母集団を同時に分析することができます．その結果，母集団間の比較，層別分析などを行えます．分析の結果，仮説モデルが当てはまった場合は，パス係数や因子平均の値などから，母集団間の違いを考察することができます．

無料体験版をダウンロード

こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．

統計的手法を身につけ，実務に生かす

イベント・セミナーのご案内

JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．

【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）

統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．

eラーニングシステム『StatCampus』のご案内

原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）

自習や集合研修に…関連書籍

実務に役立つシリーズ 第5巻 『アンケート調査の計画・分析入門』
	企業でのアンケート調査・企画や，学生向けの実証的方法の組み立て方を解説
	棟近雅彦 監修 / 鈴木督久・佐藤寧 著
	定価 3,190円（税込）
実務に役立つシリーズ 第6巻 『SEM因果分析入門』
	品質管理分野での事例を中心として，SEM因果分析を解説
	棟近雅彦 監修 / 山口和範・廣野元久 著
	定価 2,860円（税込）
	サンプルデータ公開中　ダウンロードへ