【ルポ】『JUSE-StatWorks/V4.0 SEM因果分析編』製品化1周年記念講演会

「JUSE-StatWorks/V4.0 SEM因果分析編」を2006年11月に発売してから早一年が経過しました．お蔭様で，大学および企業の技術開発，商品企画，開発設計を中心に普及しております．

さて弊社では，来る2007年7月19日（木）に“『JUSE-StatWorks/V4.0 SEM因果分析編』製品化1周年記念講演会”を開催し，構造方程式モデリング（SEM）の分野の世界的な権威であり「EQS™ 6 for Windows」の開発者でもあるピーター・M・ベントラー教授（UCLA）と，日本における構造方程式モデリング（SEM）の研究・普及の第一人者である狩野裕教授（大阪大学）にご講演頂きました．

当日は，100名以上の方々が参加されました．ここでは，講演会ルポとして，ピーター・M・ベントラー教授，狩野裕教授の講演内容をご紹介いたします．

講演会概要

開催日：2007年7月19日（木）

司会
渡邉美智子教授
（東洋大学）

プログラム
時間	タイトル	講演者
13:00～ 13:15	開会のご挨拶	(株)日本科学技術研修所代表取締役社長
13:15～ 14:20	【講演】 SEMとGMによる因果推論（入門）	大阪大学大学院基礎工学研究科狩野裕教授
14:20～ 15:00	【製品紹介】 StatWorks/V4.0 SEM因果分析編の機能概要およびデモンストレーション	(株)日本科学技術研修所数理事業部犬伏秀生
15:15～ 16:45	【特別講演】 Statistical Analysis of Correlated Processes	カルフォルニア大学ロサンゼルス校（UCLA）ピーター・M・ベントラー教授
16:45～ 17:00	質疑応答

会場の様子と講演内容

【講演】SEMとGMによる因果推論（入門）狩野裕教授（大阪大学）

狩野教授は初めに，2006年9月に開催された『JUSE-StatWorks/V4.0 SEM因果分析編製品発表会』で記念講演された筑波大学椿広計先生の講演録*1を例にひいて，以下のように期待感を表明し，講演をスタートさせました．
「『構造方程式モデリング（SEM）とグラフィカルモデリング（GM）との結合』が『科学技術分野で活用されるまでにはまだ時間がかかるかもしれませんが，技術者が創造的に考える新SQCのツールに育つのではないか』」

講演では，まず，構造方程式モデリング（SEM）とグラフィカルモデリング（GM）の統計的アプローチ方法を比較し，構造方程式モデリング（SEM）が多くの変数間の因果関係を「検証的」に分析するのに対し，グラフィカルモデリング（GM）は多くの変数間の因果関係を「探索的」に分析するものであると，2手法の違いをズバリ指摘されました．

構造方程式モデリング（SEM）は先行研究に基づく十分な固有技術情報や仮説をもとにパス図を描き，得られたモデルをデータで検証することができるので，結論に対する再現可能性が高くなります

SEMによる推定結果の一例

一方，グラフィカルモデリング（GM）は，固有技術情報は理論的には不要で（ただし，有向独立グラフの変数の順序などを考える場合には，固有技術がある程度必要になります），観測変数の因果関係をいろいろな形で探索し，その結果多くの情報を得ることができますが，結論に対する再現可能性はそれほど高くなりません．

構造方程式モデリング（SEM）では，因子分析と同様に，直接観測できない潜在変数を導入し，その潜在変数と観測変数との間の因果関係を仮定することで様々な社会現象や自然現象を理解することができます．数理的には因子分析と多重回帰分析（パス解析）を統合したモデルアプローチであるとも言え，モデルの妥当性の検討，修正への示唆，因果の大きさや強さを推定し検定することができる優れた特長を持っています．

しかしながら，交絡変数の存在や標本の偏り，測定誤差の存在などは解析上の「強敵」であり，変数間の因果関係を明確にすることや，誤差の分離，次元の縮小などの処置が必要となると語っています．

さて，製造・開発の現場では要因分析や予測・制御のためによく使われている重回帰分析ですが，構造方程式モデリング（SEM）との関係で見ると，重回帰分析は常に飽和モデルであり，説明変数間に設定された因果構造を生かすことができません．また，パス解析では，観測変数の間にある因果関係を多段階の重回帰分析の繰り返しとみなして，その因果関係を求めることができますが，構造方程式モデリング（SEM）を用いると，このような多段階の分析を1つのモデルとして分析実行することができます．

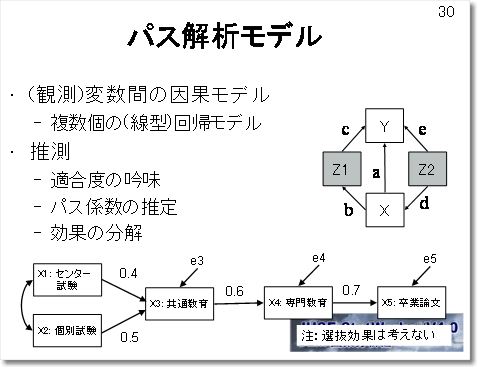
パス解析モデル

また，グラフィカルモデリング（GM）は探索的な統計的因果推論の道具であり，条件付き独立の概念を利用して，偏相関係数をみながら観測変数の直接的な関係を探索する，きわめて有用な手法であると述べられました．したがって，構造方程式モデリング（SEM）とグラフィカルモデリング（GM）に解析手法上の優劣があるわけではなく，グラフィカルモデリング（GM）は因果仮説の探索に，構造方程式モデリング（SEM）は固有技術に基づく十分な因果仮説があるときに，その仮説を検証するための有効な方法論となります．

このように両者では適用する状況が異なるので，その特徴をふまえ利用することが肝心であるとのことでした．

最後に，JUSE-StatWorks/V4.0因果分析編は，構造方程式モデリング（SEM）とグラフィカルモデリング（GM）の機能を兼ね備えた統合ソフトであり，今後の活用が大いに期待されると述べ，講演を締めくくりました．

※ 本稿は，SEM記念講演会における狩野教授のご講演をお聞きし，日科技研で取りまとめたものです

*1: 『JUSE-StatWorks/V4.0 SEM因果分析編製品発表会』で講演された椿広計氏の発表資料は，pdfファイルでご覧いただけます．
「共分散構造分析は，自然科学からモノつくりへ」椿広計氏（筑波大学大学院ビジネス科学研究科）

【特別講演】Statistical Analysis of Correlated Processes
ピーター・M・ベントラー教授（UCLA 心理学科教授）

共分散構造解析ソフトウェア「EQS™」の開発者．

構造方程式モデリング（SEM）などの研究の第一人者として活躍．日本国内でも，講演やセミナー等の普及活動を積極的に行う．

本講演では，「JUSE-StatWorks/V4.0 SEM因果分析編」のベースとなっている共分散構造分析ソフトウェア「EQS™」を使って，構造方程式モデリング（SEM）の実用性や使用上の注意点が説明されました．

構造方程式モデリング（SEM）は現象を適切にモデル化することにより，観測データから因果的効果の定量的評価を行う手法です．構造方程式モデリング（SEM）の枠組みの下で，様々なモデルを取り扱うことができます．また，分析をするにあたっては，予め分析に使用する観測データを吟味したり，構造方程式モデリング（SEM）適用後に，観測データがモデルに当てはまっているかどうかを確認したりすることが重要になります．

ここでは，それらを中心にご紹介します．

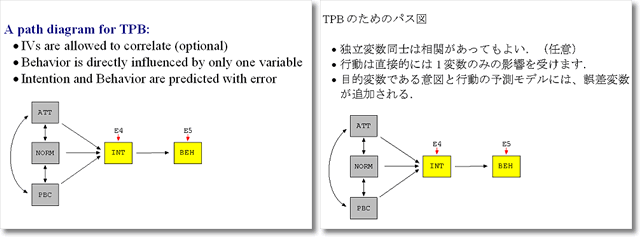
ベントラー教授の発表資料の一部（左：原文/右：和訳）　画像を拡大表示

1. 構造方程式モデリング（SEM）で取り扱うことのできる様々なモデルについて

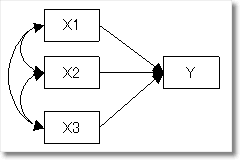
回帰分析モデル

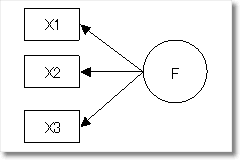
因子分析モデル

構造方程式モデリング（SEM）で取り扱うことのできるモデルに回帰分析や因子分析などがあります．

普段，よく使われている回帰分析は構造方程式モデリング（SEM）のモデルの一つとなります．ただし，回帰分析は適合度検定ができないため，一般に他のモデルより得られる情報は少なくなります．

また，因子分析は潜在変数を取り入れた構造方程式モデリング（SEM）のモデルということもできます．スピアマンは知能テストをして，知能テストの結果間に正の相関があるということを見出しました．そして，知能テストに影響を与える「IQ」という概念が背後にあるのではないかと考えました．「IQ」は現在では「言語」や「数量的な力」，「空間配置能力」などのいくつかの能力に分かれており，それらがテストの結果に影響を与えている，という考え方に発展しています．この「言語」・「数量的な力」・「空間配置能力」のように直接観測できない概念的な変数を潜在変数といいます．

次に，因子分析と主成分分析の違いについて補足します．因子分析はモデルの1つですが，これに対して，主成分分析はモデルではなく，観測変数の線形結合による記述となります．因子分析はモデルが適合しないと棄却されパラメータが求まらないことがあるのですが，主成分分析ではどんな場合でも結果が求まります．

2. 構造方程式モデリング（SEM）を使用する上での注意点

構造方程式モデリング（SEM）は，観測データから計算された分散共分散行列とモデルの分散共分散行列の違いが小さくなるようにパラメータを推定します．推定はデータの外れ値に敏感であり，外れ値があった場合に，推定できないことがあります．また，共分散や相関が非常に小さいデータ表に対して，構造方程式モデリング（SEM）を使うのは適切ではありません．実際には0.3～0.5以上の相関が必要となります．そのため，分析の前にはデータの吟味をきちんと行わなければいけません．

また，構造方程式モデリング（SEM）を適用する際には，パラメータを推定するだけではなく，観測データがどれぐらいモデルに当てはまっているかを，適合度検定を行って調べることが重要です（回帰分析では自由度が0のため，適合度検定ができないことに注意して下さい）．適合度検定の他に，CFI，AGFIなどの適合度指標を使って，観測データが真のモデルからどの程度乖離しているかを評価することもできます．

3. EQS™の設計思想を引き継ぐJUSE-StatWorks/V4.0 SEM因果分析編

EQS™のパス図描画機能では，パレット上に変数や因果的効果などを表すオブジェクトを配置するだけで，簡単にモデルを作成することができます．また，EQS™にはモデルウィザードの機能があり，いくつかの典型的なモデルを簡単な操作で構築できます．

例えば多重指標モデルを作成する場合，ウィザードに従って，まずモデルに含める潜在変数とその指標（潜在変数が影響を与える観測変数）を指定し，その後，潜在変数間の因果関係を指定すればよいことになります．このEQS™の使いやすいモデル作成機能はJUSE-StatWorks/V4.0 SEM因果分析編にも引き継がれていますので，ぜひご利用下さい．

※ 本稿は，SEM記念講演会におけるピーター・M・ベントラー教授のご講演をお聞きし，日科技研で取りまとめたものです

【製品紹介】JUSE-StatWorks/V4.0 SEM因果分析編の紹介

「JUSE-StatWorks/V4.0 SEM因果分析編」は，2006年11月に発売を開始したJUSE-StatWorksシリーズのパッケージです．構造方程式モデリング（SEM），グラフィカルモデリング（GM）により，変数間の因果関係の分析を行うことができます．回帰分析から一歩進んだ分析を行いたい方に最適なパッケージとなります．

製品の価格，稼働環境など詳細な情報は，製品ページをご覧ください．
JUSE-StatWorks/V5

機能の特徴
データ	生データ形式，分散共分散行列（相関係数行列）形式のデータを分析することができます．
予備解析機能	基本統計量，相関係数行列，多変量連関図などを出力することができます．
SEMの機能	全般	プロジェクトファイルで，データ，パス図，分析結果を1つにまとめて管理することができます．多母集団の同時分析，平均構造のあるモデルの分析も行うことができます．
	パス図	パス図作成ウィザード機能など，パス図作成のための多くの支援機能が用意されています．パス図上にパラメータ推定値を表示することができます．パス図をExcel上にMicrosoft描画オブジェクトとして出力することができます．
	分析結果	適合度指標（カイ二乗値，GFI，AGFI，NFI，CFI，AIC等），パラメータ推定値，効果の分解などが出力されます．
GMの機能	全般	プロジェクトファイルで，データ，共分散選択，グラフを1つにまとめて管理することができます．
	共分散選択	無向独立グラフ，連鎖独立グラフ，有向独立グラフに対する共分散選択を行うことができます．逸脱度，適合度指標（GFI，AGFI，NFI，SRMR）が出力されます．
	グラフ	線，矢線は偏相関係数の絶対値に応じて異なる太さ，線種で表示されます．連鎖独立グラフ，有向独立グラフの場合は，群毎に変数を着色することができます．

※: 掲載されている著作物の著作権については，制作した当事者に帰属します．; 著作者の許可なく営利，非営利，イントラネットを問わず，本著作物の複製，転用，販売等を禁止します．; 所属・役職・内容等は，当時のものです．

メールマガジン

イベント案内や製品などの最新情報をお届けします

【ルポ】『JUSE-StatWorks/V4.0 SEM因果分析編』製品化1周年記念講演会

講演会概要