主成分分析とは（多変量解析）
主成分分析とはn個の対象（サンプル）について，多数個のp変数x1，x2，…，xpのデータが観測されているとき，その対象の特徴をできるだけ少数の総合指標で記述したり，もとの変数間の相関関係を分析したりするための代表的多変量解析手法になります．
主成分分析の使用方法
1. データの用意
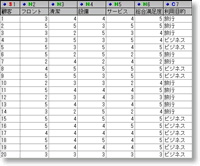
図1. ホテルのお客様満足度調査データ
（画像クリックで拡大表示）
ホテルのお客様満足度の調査のため，宿泊客を対象にアンケートをおこなって得た回答データがあります．
1列目は顧客番号であり，2列目はフロント，3列目は清潔，4列目は設備，5列目はサービス，6列目は総合満足度に対して5段階評価（1：不満，2：やや不満，3：どちらともいえない，4：やや満足，5：満足）をしたものです．7列目は利用目的（質的変数）です．
主成分分析を用いて2列目から6列目までの5つの量的変数の情報を集約してみましょう．
2. 変数の指定
図2. 変数の指定
（画像クリックで拡大表示）
メニューバーから[手法]-[多変量解析]-[主成分分析]を起動し，変数の指定画面でサンプル名と量的変数の全変数を指定します（ここで質的変数は指定できません）．
3. 出発行列の指定
図3. 出発行列の指定
（画像クリックで拡大表示）
出発行列を選択します．
出発行列として「相関係数行列」か「分散共分散行列」が指定できます．共通の測定単位を持ったデータで変数のばらつきを重視して主成分を求めたい場合は分散共分散行列を指定しますが，通常は相関係数行列を指定します．
ここでは相関係数行列を指定します．
4. 基本表示
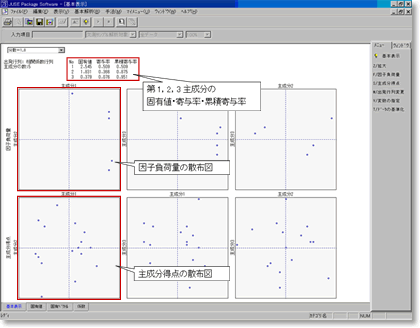
主成分分析の「基本表示」ウィンドウが表示されます．ここで第1，2，3主成分の固有値・寄与率・累積寄与率と，因子負荷量の散布図，主成分得点の散布図を見ることができます．
図4. 基本表示（画像クリックで拡大表示）
5. 固有値の確認
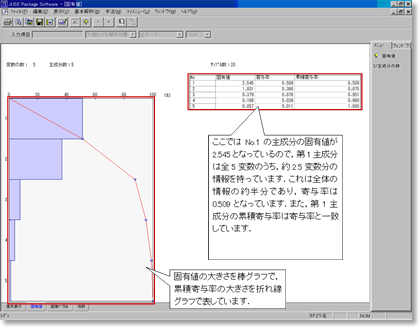
「固有値・寄与率・累積寄与率」の詳細は「固有値」ウィンドウで確認することができます．画面下にある「固有値」タブを選択してください．
「基本表示」ウィンドウでは第3主成分までの固有値・寄与率・累積寄与率しか見られませんでしたが，ここでは全主成分の固有値・寄与率・累積寄与率が確認できます．固有値は各主成分にどの程度の情報が集約されているかを見る指標であり，寄与率は全体の持つ情報のうち，どの程度の情報がその主成分で表されているかを見る指標です．累積寄与率は寄与率の累積を求めたものです．
図5. 固有値（画像クリックで拡大表示）
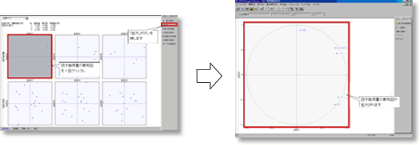
6. 因子負荷量散布図の拡大
次に因子負荷量の散布図を拡大してみましょう．
「基本表示」ウィンドウに戻り，主成分1と主成分2の因子負荷量の散布図（左上の散布図）をクリックし反転させた状態で，メニューボタンの「拡大」を押します．
図6. 因子負荷量散布図の拡大（画像クリックで拡大表示）
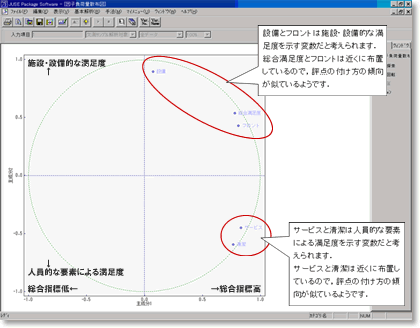
7. 因子負荷量散布図の解釈
因子負荷量は主成分と元の変数との相関係数です．
第1主成分はすべて正の値になっています．よって第1主成分は総合指標を表すものだと解釈できます．第2主成分は設備，総合満足度，フロントが正の値で，サービス，清潔が負の値となっております．よって上方が施設・設備的な満足度，下方が人員的な要素による満足度を示すものだと考えられます．また，近くに布置する変数同士は相関が強いことを意味しています．総合満足度とフロント，サービスと清潔は評点の付け方の傾向が似ているようです．
図7. 因子負荷量散布図の解釈（画像クリックで拡大表示）
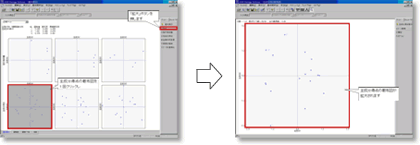
8. 主成分得点散布図の拡大
今度は主成分得点の散布図を拡大してみましょう．「基本表示」ウィンドウに戻り，主成分1と主成分2の主成分得点の散布図（左下の散布図）をクリックし反転させた状態で，メニューボタンの「拡大」を押します．
図8. 主成分得点散布図の拡大（画像クリックで拡大表示）
9. 散布図の設定変更
図9. 散布図の設定変更
（画像クリックで拡大表示）
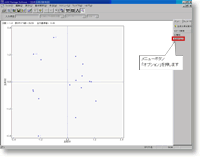
より詳細に主成分得点をチェックするために，散布図の設定を変更します．
主成分得点の散布図が拡大された状態で，メニューボタン「オプション」を押します．
「主成分得点 散布図オプション」ダイアログが表示されます．
「目盛り変更」タブで「ベクトル表示」にチェックを付け，「項目名」タブで表示範囲を「全範囲」に設定し，「OK」ボタンを押します．こうすると，主成分得点の散布図上に因子負荷量のベクトルと全プロットのサンプル名（顧客番号）を表示できるようになります．
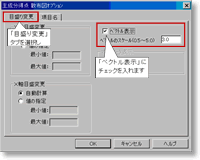 図10. ベクトル表示の設定 （画像クリックで拡大表示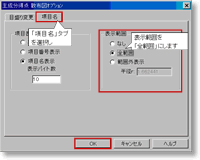） |  図11. 項目名表示の設定 （画像クリックで拡大表示） |
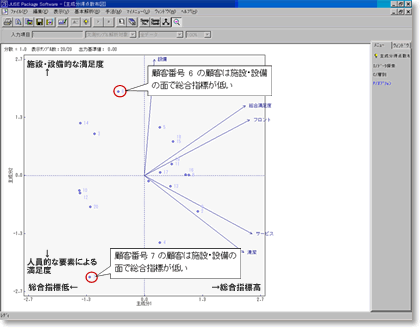
10. 主成分得点散布図の解釈
主成分得点散布図から特徴的なサンプルを探します．
例えば，顧客番号6の顧客は施設・設備の面で総合指標が低いようです．また，顧客番号7の顧客は人員的な要素の面で総合指標が低いようです．他と傾向が少し違っている6と7の顧客に，ホテルの満足度について詳しく意見を聞いてみるといいかもしれません．
図12. 主成分得点散布図の解釈（画像クリックで拡大表示）
11．固有ベクトル・係数
他のウィンドウの説明をします．
「固有ベクトル」ウィンドウでは，各主成分の固有ベクトルを一覧表示します．固有ベクトルは主成分を構成する際の各変数に対する重みであり，得られた主成分が何を表すのかを解釈する際に利用できます．しかし多くの場合，解釈のしやすさから主成分と元の変数との相関係数である因子負荷量が用いられます．
「係数」ウィンドウでは，主成分得点を計算する式の元の変数への係数を表示しますが，この係数は結果の解釈にはあまり用いません．
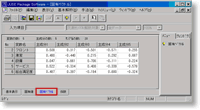 図13. 固有ベクトル （画像クリックで拡大表示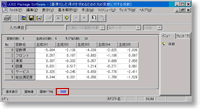） |  図14. 係数 （画像クリックで拡大表示） |
よくあるご質問（回帰分析・多変量解析）FAQをもっと見る
本システムの機能・特徴
- 層別
- 主成分得点散布図を拡大した状態でメニューボタン「層別」を押し，層別変数を指定すると，主成分得点を層別して表示することができます．
※ 「画面はJUSE-StatWorks/V4.0のものです」
無料体験版をダウンロード
こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．
統計的手法を身につけ，実務に生かす
イベント・セミナーのご案内
JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．
- 【セミナー】多変量解析入門
- 多変量解析の基礎教育として最適なコースです．
- 【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）
- 統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．
- eラーニングシステム『StatCampus』のご案内
- 原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）
| JUSE-StatWorksによる新品質管理入門シリーズ 第5巻 『多変量解析入門』 | |
|---|---|
 |
「多変量解析編」や「市場調査分析編」から，よく使われる9手法を解説 |
| 棟近雅彦 監修 / 野澤昌弘 著 | |
| 定価 3,080円（税込） | |
| 書籍用体験版とサンプルデータ公開中 ダウンロードへ | |
イベント案内や製品などの最新情報をお届けします