1. ホーム
2. ＞統計解析・品質管理
3. ＞製品案内
4. ＞手法一覧

単回帰分析とは（回帰分析）

単回帰分析の目的は，ある変数y(目的変数)が変数x（説明変数）に対してどの程度変化しているか，または信頼できるかを予測し明らかにするためのものです．数多くある統計手法のうち，最も頻繁に用いられているのは回帰分析です．

単回帰分析とは，yを目的変数，xを説明変数1つとして，
y＝β0＋β1x＋ε
の式によって現象を説明しようとする手法です．この式を回帰式と呼びます．
ここでは，β0を定数，β1を回帰係数，εを誤差と呼び，εはxでは説明しきれない部分を示しています．また，誤差は，平均0，分散σ2の正規分布に従うと仮定しています．

---

検定・推定を用いた事例をご覧いただけます．

清水 貴宏氏（松下電器産業株式会社）のシンポジウムでの発表事例

ものづくりにおける単回帰分析の必要性と活用

単回帰分析の使用方法

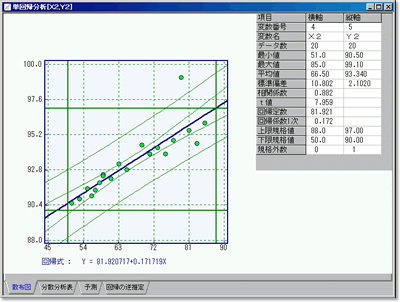
散布図上には，各種統計量，回帰式，回帰直線，回帰線の信頼区間線，データの信頼区間線，格子線，規格線(説明変数，目的変数ごと)の表示など，実務解析で役に立つオプション機能を数多く搭載しました．

回帰は1次モデルまたは2次モデルの何れかを指定することができます．

（画像クリックで拡大サイズへ）

データ探索では，グラフ上のプロット点あるいはあらかじめ検討したい特別なサンプルに対し，画面上にサンプル番号を表示したり，データを一時的に解析から除くマスクを指定することができます．

（画像クリックで拡大サイズへ）

分散分析表は，用いたデータに直線を当てはめることに意味があるかどうかの統計的判断の1つの目安です．目的変数yの変動を回帰平方和（SR）と残差平方和（Se）に分解し，自由度，分散，分散比および検定結果を表示します．検定結果が，有意の場合には，統計的に使用したデータの範囲内において直線を当てはめる意味があると判断できます．

（画像クリックで拡大サイズへ）

残差のヒストグラム機能を用いて，残差が0を中心とした正規分布をしているか否か(不偏性，正規性，等分散性))をチェックすることができます．

（画像クリックで拡大サイズへ）

残差の時系列グラフ機能を用いて，残差の系列がランダムであり，サンプル順に傾向があるかどうかをグラフとタービン・ワトソン比の値で確認することができます．

（画像クリックで拡大サイズへ）

残差との連関図を用いて，残差と説明変数が無関係の状態か(独立性)を視覚的にチェックすることができます．

（画像クリックで拡大サイズへ）

よくあるご質問（回帰分析・多変量解析）FAQをもっと見る

• 残差の検討をおこなって得られた回帰分析結果は，その後どのように利用したらよいのでしょうか？
• 表示された回帰係数で回帰式を作ると当てはまりが良くない場合があります．有効桁数を増やす方法はありますか？

本システムの機能・特徴

単回帰分析の主なオプション機能

機能	内容
散布図	指定した変数を用いて単回帰式を当てはめた散布図が表示されます．画面には，散布図（両変数の最小値，最大値でスケーリング）上に回帰直線および母回帰，個々のデータの95％信頼区間を表示します．画面右側には，説明変数x，目的変数yの各統計量，回帰式，標準誤差が表示されます．
分散分析表	用いたデータに直線を当てはめることに意味があるかどうかの統計的判断の1つの目安になります．目的変数yの変動を回帰平方和（SR）と残差平方和（Se）に分解し，自由度，分散，分散比および検定結果を表示します．
残差の検討	求められた回帰式の妥当性の検討することができます．残差の検討では，残差の一覧表，残差のヒストグラム，残差の時系列グラフ，残差との連関図，テコ比とt値の散布図，t値のヒストグラムといった機能で，残差を様々な角度から検討できます．
予測	求められた回帰式が有効と判断されれば，説明変数xの値からモデル式より目的変数yの値や信頼区間などを予測することができます．
回帰の逆推定	求めた回帰式を変換して，目的変数yの値から逆に説明変数xを推定する場合に使用します．yに規格値が設定されている場合に用いると便利です．データの検索 散布図より任意のデータを探索します

---

※ 「画面はJUSE-StatWorks/V4.0のものです」

無料体験版をダウンロード

こちらの手法を搭載した 「JUSE-StatWorks」の体験版をお試しください．

統計的手法を身につけ，実務に生かす

イベント・セミナーのご案内

JUSE-StatWorksをご購入いただいた方や有償サポートサービス契約者の方には，割引サービスがあります．また，学生，教員，研究機関職員の方向けのアカデミック価格もございます．

【セミナー】多変量解析入門

多変量解析の基礎教育として最適なコースです．

【セミナー】StatWorks/V5操作入門（対象JUSE-StatWorks購入で受講料無料）

統計解析入門者におすすめのセミナーを定期的に開催しております．パソコン・ソフトは弊社で用意いたしますので，ソフトをお持ちでない方もお気軽にご参加ください．

eラーニングシステム『StatCampus』のご案内

原則毎月1日開講で受講期間は3か月間
eラーニングでStatworksの操作方法や，手法理論解説のコースを提供いたします．コンテンツの一部の無料体験や各種割引もございます（JUSE-StatWorks購入，有償サポートサービス契約者など）

自習や集合研修に…関連書籍

JUSE-StatWorksによる新品質管理入門シリーズ 第4巻 『回帰分析入門』
	「回帰分析」の基本から応用のしかたまで，丁寧に解説
	棟近雅彦 編著 / 奥原正夫 著
	定価 3,080円（税込）
	書籍用体験版とサンプルデータ公開中　ダウンロードへ