第13話 ヒストグラムと度数の度数?(六一学者の千字一話)


六一学者 - 吉澤 正氏
(第10回JUSEパッケージ活用事例シンポジウムにて)
明けましておめでとうございます.お年玉年賀はがきの当たり具合はいかがでしたか.六一学者は小吉でした.ちなみに,今年の4等の番号は,末尾が43,54,58.
さて,下2桁の00から99の100とおりがランダムに出てくるとすれば,それぞれの番号が現れる枚数の分布は,個別には,確率が100分の1の二項分布であるが,合計枚数が限られていると,100項の多項分布に従うことになる.今年の分布状況を調べてみたら表13-1のようになった.このデータの総数は501枚であるが,番号によっては“14”や“83”のように0枚の場合もある.最大は“03”と“30”の12枚.
| *=0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 合計 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0* | 6 | 6 | 4 | 12 | 5 | 3 | 8 | 3 | 4 | 5 | 56 |
| 1* | 9 | 8 | 7 | 1 | 0 | 2 | 7 | 5 | 6 | 2 | 47 |
| 2* | 7 | 5 | 4 | 4 | 9 | 5 | 4 | 9 | 3 | 6 | 56 |
| 3* | 12 | 5 | 5 | 4 | 8 | 2 | 7 | 4 | 5 | 6 | 58 |
| 4* | 6 | 5 | 3 | 4 | 4 | 8 | 6 | 1 | 6 | 5 | 48 |
| 5* | 8 | 1 | 4 | 6 | 6 | 2 | 4 | 3 | 4 | 4 | 42 |
| 6* | 3 | 4 | 6 | 4 | 6 | 8 | 9 | 9 | 3 | 3 | 55 |
| 7* | 6 | 8 | 4 | 3 | 4 | 4 | 11 | 5 | 3 | 3 | 51 |
| 8* | 7 | 6 | 4 | 0 | 4 | 2 | 2 | 7 | 6 | 5 | 43 |
| 9* | 4 | 7 | 3 | 3 | 4 | 4 | 9 | 3 | 4 | 4 | 45 |
表13-1には,ばらついた100個の度数が観察されているので,その分布を調べてみたくなる.度数の度数をとるわけである.その結果は以下のとおりである.
| 出現数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 度数の度数 | 2 | 3 | 6 | 14 | 25 | 12 | 15 | 7 | 7 | 6 | 0 | 1 | 2 |
このような分布を度数の度数(frequency frequency)ということがある.これの平均と分散は,それぞれ5.01と5.75である.毎年のデータでもこの程度に平均と分散が近い値をとっている.平均と分散が等しいのはポアソン分布の特徴で,確率の小さい稀に起こるような現象での出現度数によく見られるものである.前回第12話で占いはこのポアソン分布の性質を利用している.
ところで,この計算やヒストグラムを書く処理をJUSE-MAソフトでやってみた.すると,とんでもないヒストグラムが現れた.そこで,オプションの機能を使って,区間数数や境界の値あるいはクラスの幅を指定して4とおりのヒストグラム書いてみた.それが,図13-1から4である.どのヒストグラムがまともでしょう?
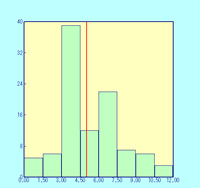 図13-1 |
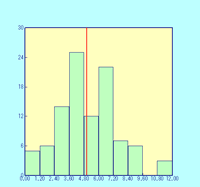 図13-2 |
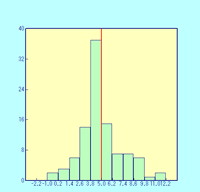 図13-3 |
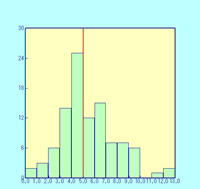 図13-4 |
ヒストグラムがおかしくなった原因は,ヒストグラムの作り方によって,一つのクラスの幅の中に,整数が一つ入ったり二つ入ったりしたことによる.このように,度数をとるデータの値が整数のときなど,一般には変数の取る値が離散的で限定されているときは,ヒストグラムはクラスの幅の取り方に気をつけないといけない.ヒストグラムを見るときにはそういうこともあると思って注意してください.
2002年1月18日掲載
イベント案内や製品などの最新情報をお届けします