新手法例 時系列分析(ARIMAモデル)の機能とその活用(株式会社日本科学技術研修所 王 克義)
こちらの内容は,第10回JUSEパッケージ活用事例シンポジウム 多変量解析・信頼性解析セッション での新製品機能紹介をまとめたものです.
1. はじめに
時系列データは,通常,時間軸上で等間隔に観測される系列的なデータ群をいう.そのため,各観測値は独立であるという通常の統計解析における仮定が成立しないので,これらの時間軸上の構造的あるいは周期的変動を考慮した特有な分析手法が必要になる.時系列分析はこれらの時系列な現象が時間とともにどのように変化していくか,将来どのようになるかを分析,予測することである.
時系列分析の目的 は以下の通りである.
- 記述 (Description)
- 時系列を図示したり,基本的な記述統計量を用いて時系列の特徴を簡潔に表現すること.
- モデル解析 (Modeling)
- 時系列モデルを推定し,時系列の特徴を捉えること.
- 予測 (Prediction)
- 現在までに得られた情報から今後の変動を予測すること.
- 制御 (Control)
- 操作可能な変数を適当に変化させ目的とする制御変数が望ましい変動をするように制御すること.
今回,StatWorks/V3.0の発売(2001年2月末予定)に際して市場調査分析手法の一つとして時系列分析(ARIMAモデルによる解析)が追加されることになるが,ここではARIMAモデルの数理的な解説とある時系列データを用いた解析により,システムの機能や特徴を述べることにする.本システムの解析対象として,量的変数1個あるいは量的変数1個とそのサンプル名(時系列情報)の対からなっている.
また,解析できるモデルは以下の通りで,AR,MA,ARMA,ARIMAモデルの時系列分析機能が用意されている.
| 定常時系列 | AR(自己回帰モデル) |
|---|---|
| MA(移動平均モデル) | |
| ARMA(自己回帰移動平均モデル) | |
| 非定常時系列 | ARIMA(自己回帰和分移動平均モデル) |
2. ARIMA(Auto Regressive Integrated Moving Average)モデルとは
ARIMAモデルはBox & Jenkins(1976)によって最初に導出された.モデルには,3つのタイプパラメータ,つまり自己回帰パラメータ(p),差分の階数(d),移動平均パラメータ(q) が含まれる.
時系列データの分析において,多くの場合,時系列の統計的な性質が時間の推移によって変化しない定常過程を前提として分析が行われる.通常,時系列分析で定常化と言うと,次に述べる統計的性質が弱定常化のことを指す.
大きさnの時系列 {y1,y2,…yn} に対して,
| 平均値 | 1 ≤ t ≤ n | |
|---|---|---|
| 分散 | 1 ≤ t ≤ n | |
| 自己共分散 | 1 ≤ t ≤ n |
すなわち,平均値,分散が観測時刻によらず一定値である時系列データである.そのため,非定常な時系列データに対しては,事前に差分変換,対数変換,平方根変換などの変換処理を行うことによって,定常化することはよく行われる.
2.1 AR(Auto Regressive)モデル
確率過程yt(時系列y1,y2,…yn)が
![]() (2.1)
(2.1)
で表されるとき,ytはp次の自己回帰過程或はAR過程と呼ばれる.そして(2.1)式をp次の自己回帰モデルあるいはARモデルという.ここでは,φj( j = 1, 2, …, p )は係数であり,εtは期待値ゼロ,分散一定のホワイトノイズ(白色雑音)である.
ARモデルでは,ある時点のデータはそれ以前のデータで推定できる.(2.1)式では,各データが以前のデータの線形結合式にあるランダム誤差が加わって観測されるということを表す.
2.2 MA(Moving Average)モデル
時系列上の各データは,過去の誤差(ランダムショック)に影響されるというモデルで,次式で表現される.
![]() (2.2)
(2.2)
ここで![]() は係数であり,εtは期待値ゼロ,分散一定のホワイトノイズ(白色雑音)である.
(2.2)式をq次のMAモデル或は移動平均モデルという.
は係数であり,εtは期待値ゼロ,分散一定のホワイトノイズ(白色雑音)である.
(2.2)式をq次のMAモデル或は移動平均モデルという.
MAモデルの各データは,以前のデータのランダムな誤差の線形結合に,現在の誤差が加わって観測されるというモデルである.
2.3 ARMA(Auto Regressive Moving Average)モデル
p次の自己回帰過程において,残差εtがq次の移動平均過程であるとき, ytは
![]() (2.3)
(2.3)
を満たす.これを次数(p,q)の自己回帰移動平均過程あるいはARMA過程と呼び,ARMA(p,q)と表す.qをゼロとしたときはARモデル,またpをゼロとしたときはMAモデルとなり,ARMAモデルはARモデルやMAモデルより一般的なモデルとなる.
2.4 ARIMA(Auto Regressive Integrated Moving Average)モデル
ARIMAモデルは非定常過程に対する時系列モデルである.上で述べたように,ARMAモデルは定常な時系列過程を前提としてきた.定常性ということは,モデル自身が発散しないということである.
ところで,時系列において平均値が時間的に変動する場合(傾向変動が見受けられる場合など)は非常によく見受けられるものであり,それらに対して,ARMAモデルはそのままでは適用できない.そのため,平均値揺動を取り除くために様々な方法が用いられるが,時系列の階差をとり,その階差時系列に対してARMAモデルを適用する.このモデルをARIMAモデルあるいは自己回帰和分移動平均モデルという.
例えば,元の時系列データ{yt:t=1,2,…,n }を取り上げると,その一次階差時系列{xt:t=1, 2, …n-1 }はつぎのように表される.
xt=yt-yt-1 (2.4)
同様に,2次の階差時系列{zt:t=1,2,…,n-2 }は
zt=xt-xt-1=(yt-yt-1)-(yt-1-yt-2) (2.5)
一般にd階差の時系列ztにARMAモデルに適用したものが,ARIMAモデルである.
ARMAモデルの場合と同様に,階差dの時系列をp次のAR,q次のMAモデルに適用したARIMAモデルをARIMA(p,d,q)と表す.
ARIMAモデルを適用するかどうかの判定は,トレンドなどの平均値揺動が存在するかどうかによるものであり,第1階差,第2階差において,平均値揺動が解消されているかどうかを検討し,みられなくなったところで階差をとり終わるということになる.dの決め方は,各階差時系列において,時系列のプロット,自己相関関数の様子をみることなどが行われる.
時系列(ARIMAモデル)分析の過程は以下のようなステップで実行される.
ステップ1(モデルの同定)
ARMAに対する時系列はまず定常でなければならない.ここでいう定常とは,データがとられている各時点で,平均や分散,自己相関が一定である状態という.非定常な系列に対しては,変数変換や,差分変換など適当な変換を行なって,定常な系列にする必要がある.通常は,時系列データが定常性を示すために,どのような変換を行ったらよいか,試行錯誤的にデータプロットや(自己相関,偏自己相関)コレログラムなどを描き判断する.
- プロットによって,時系列データが定常かどうかを判断する.差分の階数を判断する.
- 自己相関(偏自己相関) コレログラムによって,時系列データには周期があるかどうかを判断する.
- 推定されるべきモデルを決める.
ステップ2(モデルの推定)
パラメータを推定する.パラメータの推定値はその次の予測の段階で,予測値とその信頼区間の計算に使用される.推定の計算は変換されたデータ系列(差分系列)に基づいて行われる.したがって,予測の段階では,差分変換を元に戻して(和分して)予測値を求める必要がある.
ステップ3(モデルの評価・診断(diagnostic checks))
この段階では,得られたモデルが適切なARIMAモデルといえるかどうかの診断と評価を行う.
注1:定常化であるかどうかは通常,時系列プロットで判断する.
注2:非定常化時系列データを定常化する方法は以下のようなものがある.
- 変数変換(データの平方根をとる,対数をとる,指数をとるなど).
- 差分をとる.
- 季節差分をとる.(なお,StatWorks/V3.0にはこの機能はない).
時系列データは経済(株価,為替,売上高,顧客数など),医療,環境(気象データ),工程管理,工業生産など種々な分野に存在する.そのため時系列分析は様々な分野で使用されており,昔から移動平均法,EPAなど数多く研究されてきた.時系列データを取り扱う場合多くは得られたモデル式を用いて,将来のある時点を予測できるようにすることが目的である.自己回帰分析過程(AR),移動平均過程分析(MA)およびそれらを結合した自己回帰移動平均混合過程分析(ARMA)などが有力な予測理論となっている.
3. 時系列分析手順と事例概要
時系列分析事例
本報告で述べる解析事例はある化学製品の産出量のデータ(「時系列入門」,W・ヴァンデール著,蓑谷,廣松,多賀出版から引用,データ数は70)である.
(1) 時系列プロットの観察
データをサンプル順に並んだプロット図を図1に示す.グラフからはほぼ定常であるとみられる.変動の幅はほぼ同じで,トレンドがなく,差分をとる必要はなさそうだ.
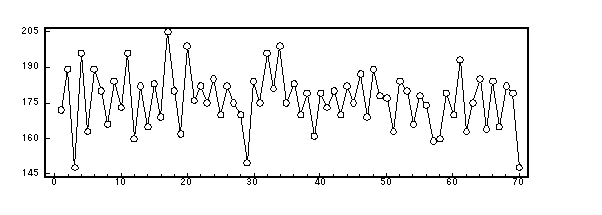
図1.時系列プロット
(2) 自己相関コレラグラムと偏自己相関コレログラムを観察
| モデル | 自己相関関数 | 偏自己相関関数 |
|---|---|---|
| AR(p) | 徐々に消滅 | ラグp以降切断 |
| MA(q) | ラグq以降切断 | 徐々に消滅 |
| ARMA(p,q) | 徐々に消滅 | 徐々に消滅 |
- MA過程の自己相関は,AR過程の偏自己相関と似た動きをしている.
- MA過程の偏自己相関は,AR過程の自己相関と似た動きをしている.
図2では,横軸をラグ(時間と対応する)として,縦軸は自己相関の数値をとる.棒グラフは自己相関係数の大きさ,二本の線は自己相関の標準誤差の1.96倍を表す.
もし,時系列データがランダム(ホワイトノイズ)なら,この時系列の母自己相関が0になるはずであり,推定された自己相関に対して,すべての母自己相関が0となる.図2をみると,ラグ1とラグ2の自己相関における絶対値は標準誤差の1.96倍より大きくなっている.そのため,ラグ1とラグ2の母自己相関が非ゼロであることがわかる.
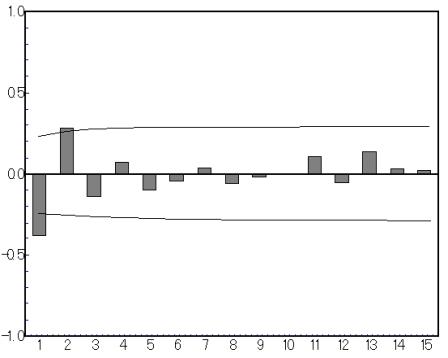
図2. 自己相関コレラグラム
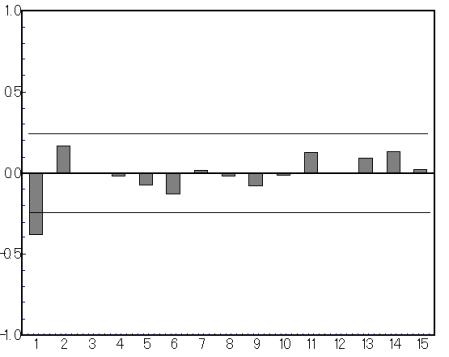
図3. 偏自己相関コレラグラム
(3) 時系列統計量による評価
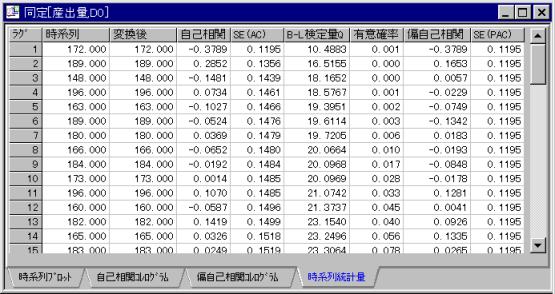
図4. 時系列統計量一覧
| 自己相関: | 0 ≤ k ﹤ n | |
|---|---|---|
| SE(AC): | 0 ﹤ k ﹤ n | |
| B-L検定量: | 0 ﹤ k ﹤ n | |
| SE(PAC): | 0 ﹤ k ﹤ n |
図4.で,B-L検定量QとはBoxなどが定義した統計量である.純粋なランダム過程,すなわちすべての自己相関が0であるモデルについて,B-L検定量Qは近似的に,自由度kのカイ2乗分布χ(k)に従う.もしQの計算値が,与えられた有意水準の値に対応する自由度kのカイ2乗統計量の分位点の値より大きければ,検定統計量を計算するために用いた自己相関の組は,ゼロと有意に異なっている.また,自己相関にある特定のパターンが存在するとされる.
図4からは,ラグ3の場合,B-L検定量Qは18.1652になっている.しかし,この仮定は純粋なランダム過程である有意水準の0.001しかない.
(4) 推定―モデル選択
導出された各時系列モデルについて,残差やAIC統計量,対数尤度,定常性,反転性などで評価し,妥当な時系列モデルを比較判断することになる.定常性はARパラメータの推定値が定常性の条件をみたすこと,反転性はMAパラメータの推定値が反転性の条件をみたすことなどを評価している.
| 自己回帰次数(p) | 移動平均次数(q) | 残差 | AIC | 対数尤度 | 定常性 | 反転性 | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 117.264 | 536.316 | 532.316 | * | - |
| 2 | 2 | 0 | 113.941 | 536.359 | 530.359 | * | - |
| 3 | 0 | 1 | 124.018 | 540.212 | 536.212 | - | * |
| 4 | 0 | 2 | 115.577 | 537.359 | 531.359 | - | * |
| 5 | 1 | 1 | 114.440 | 536.688 | 530.688 | * | * |
(5) 推定―モデル係数
ここでは,それぞれのモデルに決定的な違いが見られなかったので,No.2のモデル式(AR(2))についてモデル係数を表示する.
| 残差平方和 | 残差自由度 | 残差標準偏差 | AIC | 対数尤度 |
|---|---|---|---|---|
| 7953.45 | 67 | 118.71 | 536.359 | 530.359 |
| パラメータ名 | 係数 | 標準誤差 | t値 | p値 |
| 定数項 | 205.612 | 1.304 | 157.67 | 0 |
| AR(1) | -0.3433 | 0.1264 | -2.72 | 0.008 |
| AR(2) | 0.1775 | 0.1264 | 1.4 | 0.165 |
yt=205.612-0.3433yt-1+0.1775yt-2+at
(6) 予測―予測図
観測値と予測値のプロットでは,データへの適合度が充分であること,予測の精度が良いことなどが評価される.図7は65個のデータから推定されたAR(2)モデル式を用いて,66から70までの5個のデータを予測し,その結果と実際の観測値を比較したプロット図である.
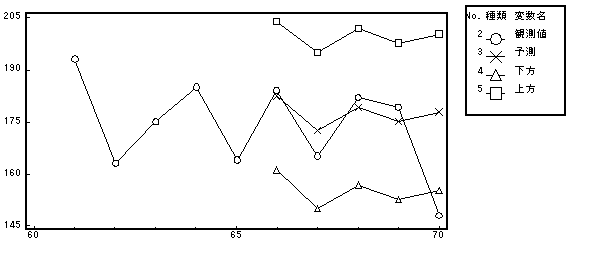
図7. 予測図画面
(7) 予測結果を観察
観測値とAR(2)モデルで予測した値の比較を 図8に示す. ケースNo.70以外はかなり近い予測を示している.
| ケースNo. | 観測値 | 予測値 | 下方95% | 上方95% |
|---|---|---|---|---|
| 66 | 184 | 182.424 | 161.0848 | 203.7632 |
| 67 | 165 | 172.3862 | 149.9639 | 194.8085 |
| 68 | 182 | 179.2162 | 156.7103 | 201.7221 |
| 69 | 179 | 175.0559 | 152.5386 | 197.5732 |
| 70 | 148 | 177.7295 | 155.2117 | 200.2474 |
(8) 残差の自己相関コレラグラム
残差に系列相関がなく,正規分布で近似できることが必要である.
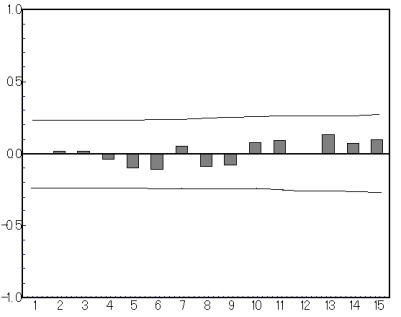
図9.残差の自己相関コレラグラム
残差の自己相関コレラグラムからは,ゼロに近く,残差に対してデータの相関が余りないと考えられる.
4. 今後の課題
今後,さらに季節変動ARIMAモデルや時系列パターンを考慮した解析などを開発していく予定である.
5. 参考文献
- 杉原敏夫,「適応的モデルによる 経済時系列分析」,工学図書株式会社,1996年.
- 廣松 毅,浪花貞夫,「経済時系列分析」,朝倉書店,1995年.
- 渡邊美智子,「はじめての時系列分析 ――ARIMAモデル入門――」,日本科学技術連盟テキスト.
- 北川源四郎,「時系列解析プログラミング」,岩波書店,1993年.
- W・ヴァンデール著,蓑谷,廣松,「時系列入門―ボックスージェンキンスモデルの応用」,多賀出版,1996年.
- George E.P.Box, Gwilym M. Jenkins, Gregory C.Reinsel, "Time Series Analysis Forecasting and Control", Prentice-Hall International,Inc, Third Edition.
- 石村貞夫,「SPSSによる時系列分析の手順」,東京図書,1999年.
- P.J.ブロックウェル/R.A.デービス著,辺見 功,田中 稔,宇佐美義弘,渡辺則生,「入門時系列解析と予測」CAP出版,2000年.
お問い合わせ
ご不明な点がございましたら,お問い合わせ窓口よりお問い合わせください.
過去のシンポジウム開催の様子や発表資料は,過去のシンポジウムプログラムおよび発表資料からご覧いただけます.
- 要旨集の販売について

- これまでに開催された各シンポジウムの発表要旨集を販売しております.ただし在庫がない場合もございますので,あらかじめご了承下さい.ご希望の方はお問い合わせ窓口よりお問い合わせください.
JUSE-StatWorks/V5の無料体験版をお試しください