第43話 三角分布族について(六一学者の千字一話)


六一学者 - 吉澤 正氏
(第10回JUSEパッケージ活用事例シンポジウムにて)
第41話では,アイルランドのベン・ブルベンの姿から台地(台形)分布族を考え,第42話では山々のモーメントということで日本の山の形を取上げた.そのついでといってはなんだが,三角分布族についても,モーメントや特性値を検討したところ,なかなか面白いこともあるので,まとめておきたい.
台地分布族は区間[0,1]での一様分布から三角分布までを一族として扱ったが,その三角分布は対称形であった.その三角分布の頂点を左右にずらしていったときの仲間を三角分布族と言おう.
確率分布であるには,密度関数の面積が1となるので,その三角分布の頂点は,高さが一定の2で,頂点のx座標がゼロから1まで動くとするのが自然であろう(図1).頂点のx座標をパラメーターとし,それをa とする(図2参照).
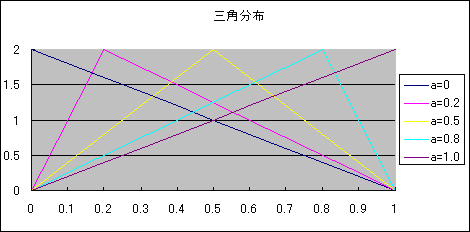
図1. 三角分布族
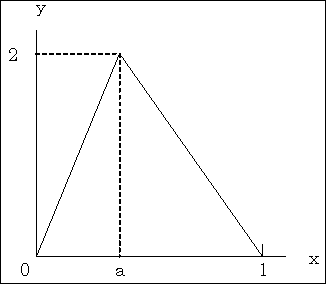
図2. 三角分布
x=aのところで頂点になり,その高さをhとすると,底辺の長さは1としたので,その面積はh/2で,三角形が確率密度関数であるには,
h / 2 = 1
として,
h = 2 …(1)
となることは明らかである.
また,三角形の左の勾配をbとすると,
b = 2 / a …(2)
とかける.右側の勾配は
- 2 / ( 1 - a ) …(3)
これより,三角分布の 確率密度関数f(x) は次のように表せる.これについて,∫f(x) dx =1 となることを積分により確認することは容易である.
(4)
| f ( x ) = | ( 2 / a )x, | 0 ≦ x < a |
| ( 2 / ( 1 -a ) ) ・ ( 1 - x ), | 1 - a ≦ x ≦ 1 |
次に,三角分布について,原点周りのモーメント,すなわち,X,X2,X3,X4の期待値を求める.その結果は以下のとおり(表1).計算は,数式処理ソフトを使うとよいだろうが,台地分布についての計算よりは簡単である.
(4)では,パラメーターaが勾配の分布にあるので,aがゼロや1のときは特別であるが,表1の結果は,そのときも適用できる.
表1. 三角分布族の原点周りのモーメント
| 平均µ = | E[X] | = ( 1 + a )/3 |
| X2の期待値 | E[X2] | = ( 1 + a + a2 ) / 6 |
| X3の期待値 | E[X3] | = ( 1 + a + a2 + a3 ) / 10 |
| X4の期待値 | E[X4] | = ( 1 + a + a2 + a3 + a4 ) / 15 |
表1をみると,大変すっきりした公式になっていて,k次のモーメントについてもすぐに予想される.aが2のときは,台地分布のときに計算してあるもの(41話の表1から表3)と比べてみると一致していることがわかる.aがゼロのときの平均は1/3,aが1のときは2/3となることももっともうなずける.
さらに,分散,標準偏差,ひずみ,とがりなどの特性を計算してみると,その結果は,表2のようになる.ひずみは,簡単な式にはならないが,とがりが-0.6と一定になることが面白い.このことは,これまでに知られていたことかどうかインターネットで調べてみたが,分散までしか出ていなかった.もうすこし調べてみたい.
なお,とがりは,正規分布のときをゼロにするように,基準化したときの4次の平均値周りのモーメントから3を引いてある.
表2. 三角分布族の特性
| 平均 | = ( 1 + a ) / 3 |
| 分散V[X] | = ( 1 - a + a2 ) / 18 *1 |
| ひずみ | = ( 1 - 2 a ) ( 2 + a - a2 ) / 270 /(標準偏差の3乗) |
| とがり | = -0.6 *2 |
- *1
- 標準偏差は分散の平方根
- *2
- 一定になることがおもしろい
この結果を数値的に示すと,表3のようになる.台地分布族のときのようにシグマ幅をつけておいた.
| a | 平均値 | 標準偏差 | 分散 | ひずみ | とがり | シグマ幅 |
|---|---|---|---|---|---|---|
| 0 | 0.333 | 0.236 | 0.056 | 0.566 | -0.6 | 4.24 |
| 0.1 | 0.367 | 0.225 | 0.051 | 0.545 | -0.6 | 4.45 |
| 0.2 | 0.400 | 0.216 | 0.047 | 0.476 | -0.6 | 4.63 |
| 0.3 | 0.433 | 0.209 | 0.044 | 0.356 | -0.6 | 4.77 |
| 0.4 | 0.467 | 0.205 | 0.042 | 0.191 | -0.6 | 4.87 |
| 0.5 | 0.500 | 0.204 | 0.042 | 0.000 | -0.6 | 4.90 |
| 0.6 | 0.533 | 0.205 | 0.042 | -0.191 | -0.6 | 4.87 |
| 0.7 | 0.567 | 0.209 | 0.044 | -0.356 | -0.6 | 4.77 |
| 0.8 | 0.600 | 0.216 | 0.047 | -0.476 | -0.6 | 4.63 |
| 0.9 | 0.633 | 0.225 | 0.051 | -0.545 | -0.6 | 4.45 |
| 1 | 0.667 | 0.236 | 0.056 | -0.566 | -0.6 | 4.24 |
ところで,三角形の大きさを一般に,図3のように,底辺をbからcとし,頂点の横軸座標をaとしておくと,その平均は
( a + b + c )/ 3
なることは,よく知られている.この式で,bをゼロ,cを1とすれば,表1の結果に一致するが,表1の公式から,一般の三角形での分散などを求めるのは,変数変換を考えればよい.図1(あるいは図2)での変数をX,図3での変数をZとすると,
X = ( Z - b ) / ( c - b )
とすればよく,表1や表2でのパラメーターaを
( a - b ) / ( c - b )
で置き換えれば,平均や分散が求められる.ちなみに,図3での分散は,
( ( c - b )2 - ( c - b ) ( a - b ) + ( a - b )2 ) / 18
あるいは,
( a2 + b2 + c2 - ab - bc - ca ) / 18
とも書ける.
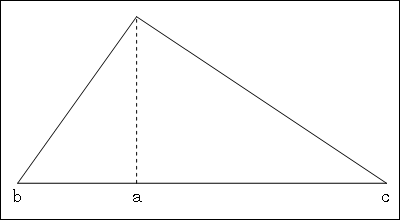
図3. 一般の三角形
- 補足
- Wikipedia には “Triangular distribution” という項があり,kurtosis(とがり)が 5/12 と示されている.これは3を引いていない数字であるが,とがりが一定になることは示されている.同じWikipedia には “Kurtosis” の項があるが,そこでは,平均値まわりの4次モーメントを標準偏差の4乗で割って3を引くものと定義してある.
イベント案内や製品などの最新情報をお届けします