第36話 ワールドカップ・グループFの体格分析(六一学者の千字一話)


六一学者 - 吉澤 正氏
(第10回JUSEパッケージ活用事例シンポジウムにて)
2006年ワールドカップ・ドイツ大会では,ジーコ・ジャパンの活躍は今ひとつであったが,世界の強豪チームの技術や猛烈な闘志に興奮をおぼえた.
日本チームの課題の一つとして,1次予選を戦ったグループFのオーストラリアやクロアチアの体格を生かしたパワープレイにやられたことがあげられた.
たまたま,大学の統計学の授業で複数のデータセットの間の分布の違いを扱っていたので,さっそく,インターネットでグループFの日本,ブラジル,クロアチア,オーストラリアの4チームの身長と体重のデータを調べて分析してみた(データは,適当なサイトからダウンロードできるが,身長と体重が,“185/82”などと,スラッシュで区切られた文字列で表示されていたので,エクセルの文字操作の関数を使って.身長と体重の数値データに変換した).
データの準備
データは,日本科学技術研修所のStatWorksで分析できるように,変数として,国名,選手名,ポジション,生年月日,身長,体重などを用い,チームごとに23人を縦の配列に並べた.国名とポジションは層別因子として質的変数で,ポジションは,GK(ゴールキーパー)DF(デフェンス),MD(ミッドフィールダー),FW(フォワード)である.国別の比較以外にポジション別の比較もできるようにした.
※ 下記URLからJUSE-StatWorks用のデータをダウンロードできます.
2006WCF.dd7(2006年ワールドカップ・グループF JUSE-StatWorks用データ)
定石の分析
まず,基本統計量として平均と標準偏差の比較,次に中央値・4分位値・最大値・最小値などの順序統計量から箱ひげ図を描く.
身長と体重について,表1に,チーム別の平均値,標準偏差,中央値を,図1に,層別ヒストグラムを,図2に箱ひげ図を示す.
各チームの特徴は,すぐに読み取れると思うが,次のように観察できる.
- 日本は,最も大きいオーストラリアに対して,身長で6センチ,体重で6キロぐらい劣っている.
- オーストラリアとクロアチアは身長では同程度であるが,体重ではオーストラリアのほうが重い.
- 標準偏差や箱ひげ図でみると,ブラジルは選手の体格でややバラツキがあり,小さい選手もまざっている.オーストラリアには2メートルを超える選手がいる.
| 国名 | 身長 | 体重 | ||||
|---|---|---|---|---|---|---|
| 平均値 | 標準偏差 | 中央値 | 平均値 | 標準偏差 | 中央値 | |
| 日本 | 178.7 | 4.1 | 178 | 74.3 | 4.4 | 74 |
| ブラジル | 181.0 | 7.4 | 183 | 76.1 | 6.6 | 75 |
| クロアチア | 184.3 | 5.6 | 184 | 78.3 | 6.2 | 78 |
| オーストラリア | 184.4 | 7.7 | 183 | 80.6 | 6.6 | 80 |
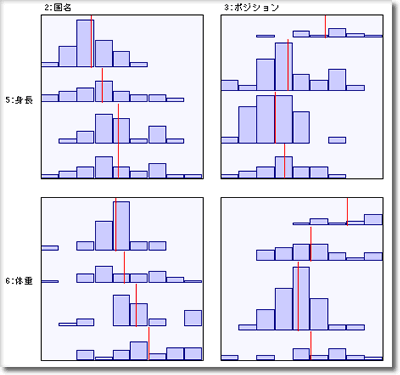
図1. 身長と体重の国ごとの層別ヒストグラム[拡大表示]
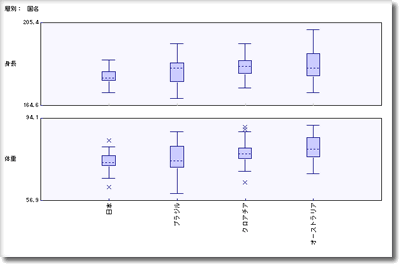
図2. 身長と体重の国別箱ひげ図[拡大表示]
多変量連関図
多変量連関図で,一度に各変数の分布や相関・連関の状態を見ることもできる(図3).ポジション別の身長や体重の比較もわかろう.
1チーム23人の登録の中で,各国がポジション別に何人をわりあてたかも帯グラフで確認できる(図4).
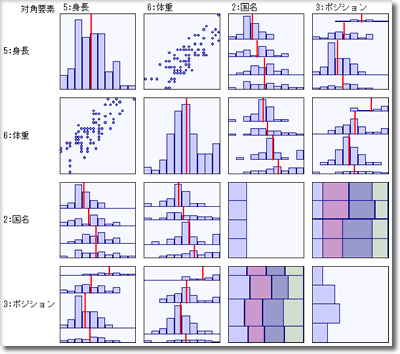
図3. 多変量連関図[拡大表示]
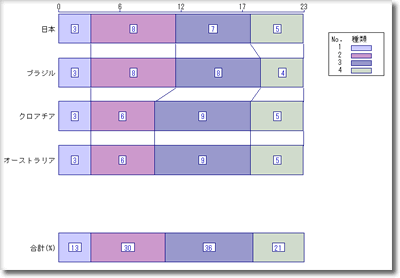
図4. ポジション別選手数の国別帯グラフ[拡大表示]
身長と体重の関係を層別散布図で見る
横軸を身長,縦軸を体重にして,身長と体重の関係をまず層別散布図でみる.
そこに回帰直線を書いてみ見ると(図5)勾配は,クロアチアが少し違うが,どのチームもほとんど同じである.
身長から見た(同じ身長で体重を比較した)体重差では,オーストラリアが少し重い感じである.散布図をチームごとに分けて表示したのが図6であるが,体重差は読み見取りにくいが,勾配はクロアチアがすこし違うように見れる.
あとで,回帰分析で,モデルを当てはめてみると,その勾配の差はほとんどないという程度であることがわかった.
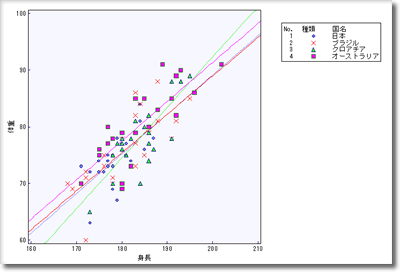
図5. 身長と体重の層別散布図(全データ,相関係数は0.79)拡大表示
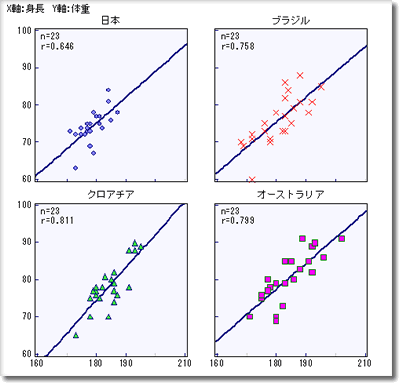
図6. 身長と体重の層別散布図(国別に表示)拡大表示
回帰分析の変数選択でモデルの検討
目的変数を体重,説明変数を身長にして,区別を層別因子として回帰分析をしてみるのもよいだろう.
StatWorksの多変量解析ソフトは,そのような問題が得意で,画面を見ながら変数選択を進めていくことができる.結論として,回帰モデルとしては,オーストラリアのダミーを入れれば(切片をオーストラリアだけ差があるとすれば),勾配については差をないというほうが妥当と思われる.回帰式は以下のとおりである.
- オーストラリア
- 体重 = 0.73 * 身長 - 57.38
- その他の国
- 体重 = 0.73 * 身長 - 55.26
このあとに
国別のほかにポジション別も入れて,2元配置データとしての分析をしてみることもおすすめしたい.
説明変数を国とポジションとして,目的変数を体重あるいは身長とする.モニタリング機能を使うとよいグラフが出る.
このあと,準決勝に残った4チームについても分析してみたが,ドイツは体格的に大きいが,イタリア,フランス,ポルトガルはブラジル並みで,日本ともそれほど差があるわけではない.
日本の一般の人のデータが手許にあったので比べてみたが,世界レベルのサッカー選手は,身長のわりに体重が相当に重いというわけでなく,よく引き締まった体格であることもわかる.
皆さんもいろいろとデータを楽しんでください.
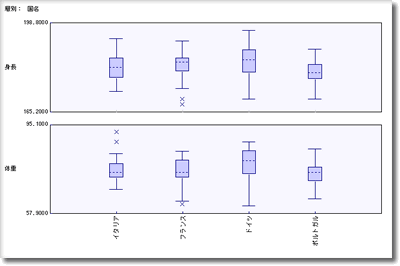
図7. ベスト4のチームの身長と体重[拡大表示]
イベント案内や製品などの最新情報をお届けします